harmonic series

math §

A divergent series:

$$\sum _{n=1}^{\infty }\frac{1}{n}$$

music §

A harmonic series (also overtone series) is the sequence of harmonics, musical tones, or pure tones whose frequency is an integer multiple of a fundamental frequency.

related: harmony

The fundamental frequency, often referred to simply as the fundamental, is defined as the lowest frequency of a periodic waveform

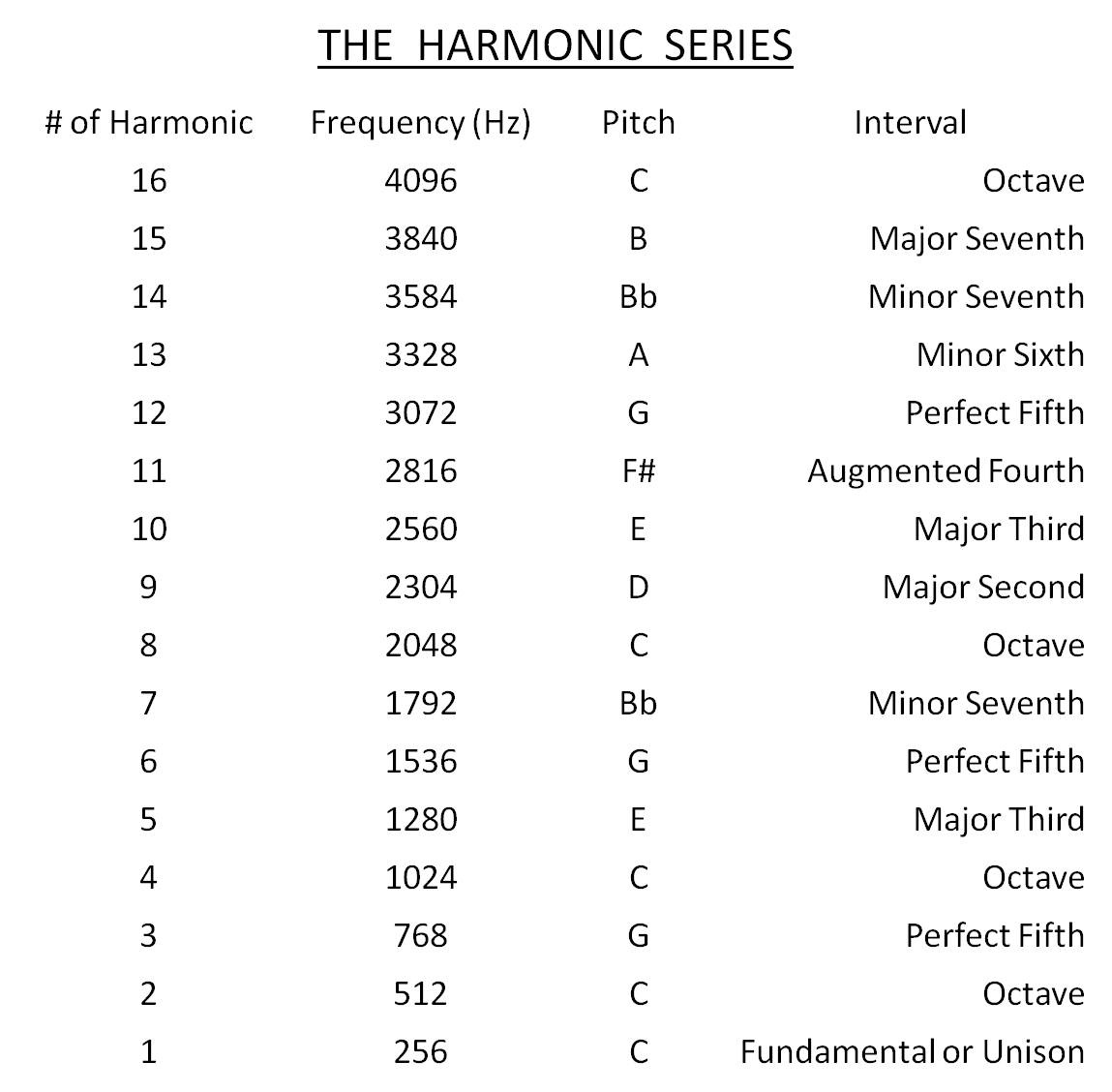
Below is a harmonic series starting on C.

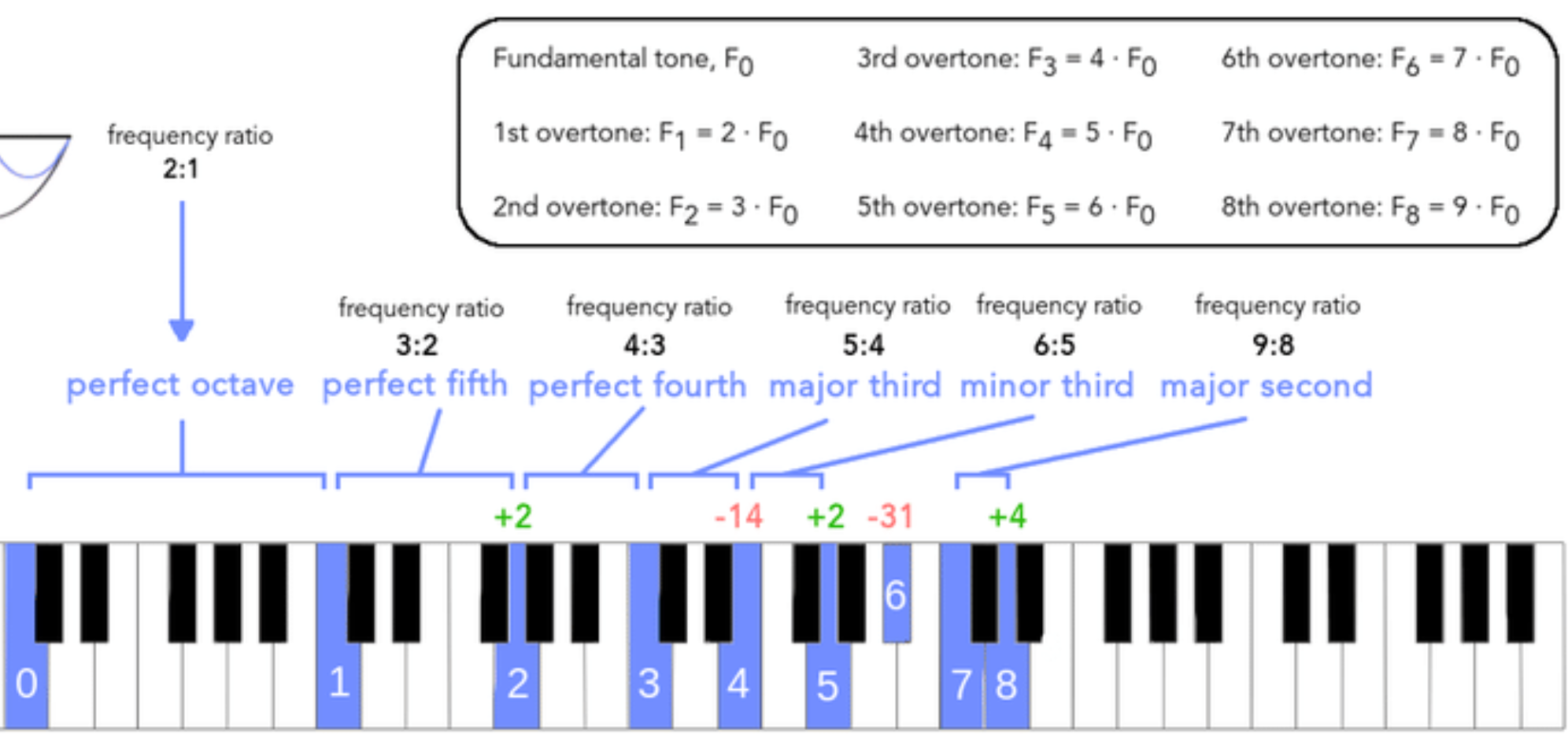
The first harmonic is the fundamental. The nth harmonic or the $(n-1)$th overtone is the fundamental frequency times n.

Note that the last column refers to the interval between the harmonic and the fundamental.

---

$A_4$ and its first 15 overtones:

---

Try it on the guitar. Pluck the $E_4$ string, there’s your fundamental or the 1st harmonic.

To find the 2nd harmonic, divide the string into two. At 1/2, you’ll find the 12th fret – $E_5$. This is an octave from the fundamental.

To find the 3rd harmonic, divide the string into 3. At 1/3, you’ll find $B_4$. This is a perfect 5th from the fundamental. Using what we’ve found above, we can find the note at 2/3 of the string. The remaining 2/3 of the string can be can be split in 2. 1/2 of the remaining string must be an octave up from $B_4$, so we have $B_5$.

To find the 4th harmonic, divide the string into 4. At 1/4, we have $A_4$. This is a perfect 4th from the fundamental. At 2/4, we have $E_5$. (Derive this by dividing the remaining 3/4 of the string into 3 and finding the note at 1/3, which is a perfect 5th up from $A_4$.) At 3/4, we have $E_6$. (Derive this by diving the remaining 2/4 of the string into 2 and finding the node at 1/2, which is an octave up from $E_5$.)

Now divide the whole string into 5 parts At 1/5, we have $G{♯}_4$. This is a major 3rd from the fundamental. At 2/5, we have $C{♯}_5$. (previous note + perfect 4th) At 3/5 we get $G{♯}_5$. (previous note + perfect 5th) At 4/5 we get $G{♯}_6$. (previous note + octave)

And so on.

---

Strings tip: bowing closer to the bridge emphasizes higher harmonics (more crisp). Bowing closer to the fingerboard emphasizes fundamental frequency (more mellow).