equal temperament

12TET, or 12 tone equal temperament is the standard tuning used today. It’s evolved from Pythagorean tuning -> just intonation -> mean tone temperament. source

How the 12-note scale came about §

Let’s try building the scale, starting with $f=440$.

We want to be able to play perfect fifths and octaves, so we’ll find new notes by going up by a fifth (multiply by 3/2), and back down an octave (divide by 2) if it goes above 880.

Go up a fifth: 440 x 3/2 = 660.

Go up another fifth to get 660 x 3/2 = 990. This is outside our octave, so we divide by 2 to get the note 495.

Go up another fifth to get 495 x 3/2 = 742.5.

Go up another fifth and down an octave to get 742.5 x 3/2 / 2 = 556.875.

…

We will have exhausted all possible notes when we return to f = 440, but this won’t happen. Proof:

There are infinitely many possible notes, so why divide an octave into 12?

After 12 applications of the ratios 3/2, we come back very close to where we started from.

(3/2)^0 = 1
(3/2)^1 = 1.5
(3/2)^2 = 1.125 (after dividing by 2)
(3/2)^3 = 1.6875 (after dividing by 2)
(3/2)^4 = 1.2656 (after dividing by 4)
(3/2)^5 = 1.8984 (after dividing by 4)
(3/2)^6 = 1.4238 (after dividing by 8)
(3/2)^7 = 1.0678 (after dividing by 16)
(3/2)^8 = 1.6018 (after dividing by 16)
(3/2)^9 = 1.2013 (after dividing by 32)
(3/2)^10 = 1.8020 (after dividing by 32)
(3/2)^11 = 1.3515 (after dividing by 64)
(3/2)^12 = 1.0136 (after dividing by 128)

This is known as the…

Pythagorean tuning §

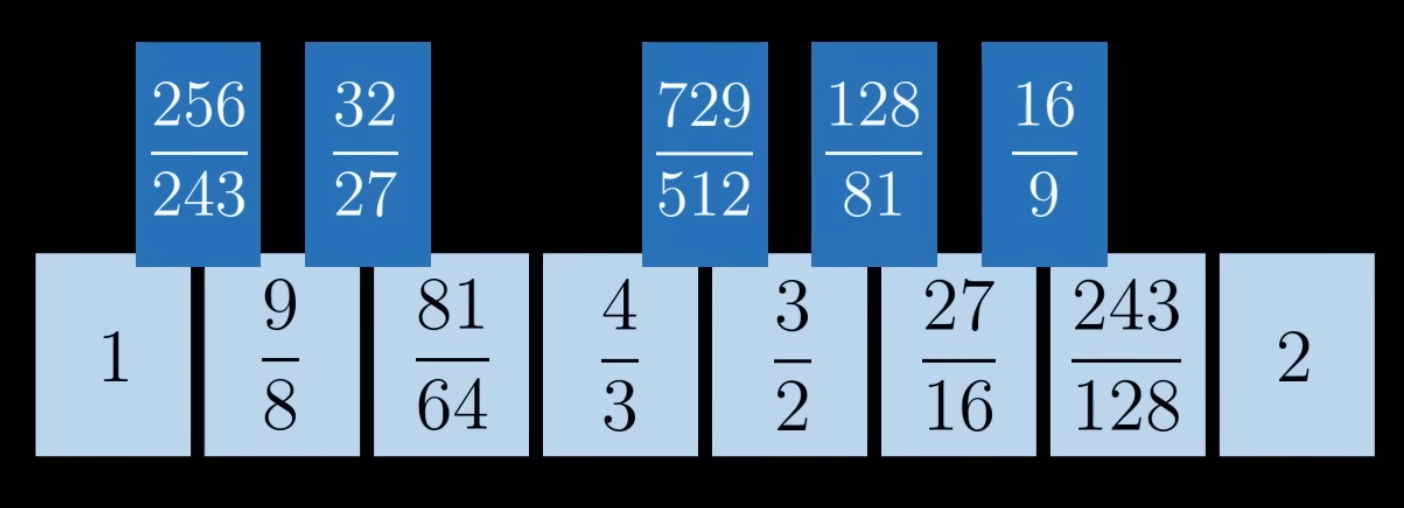
We see that they are quite unevenly spaced:

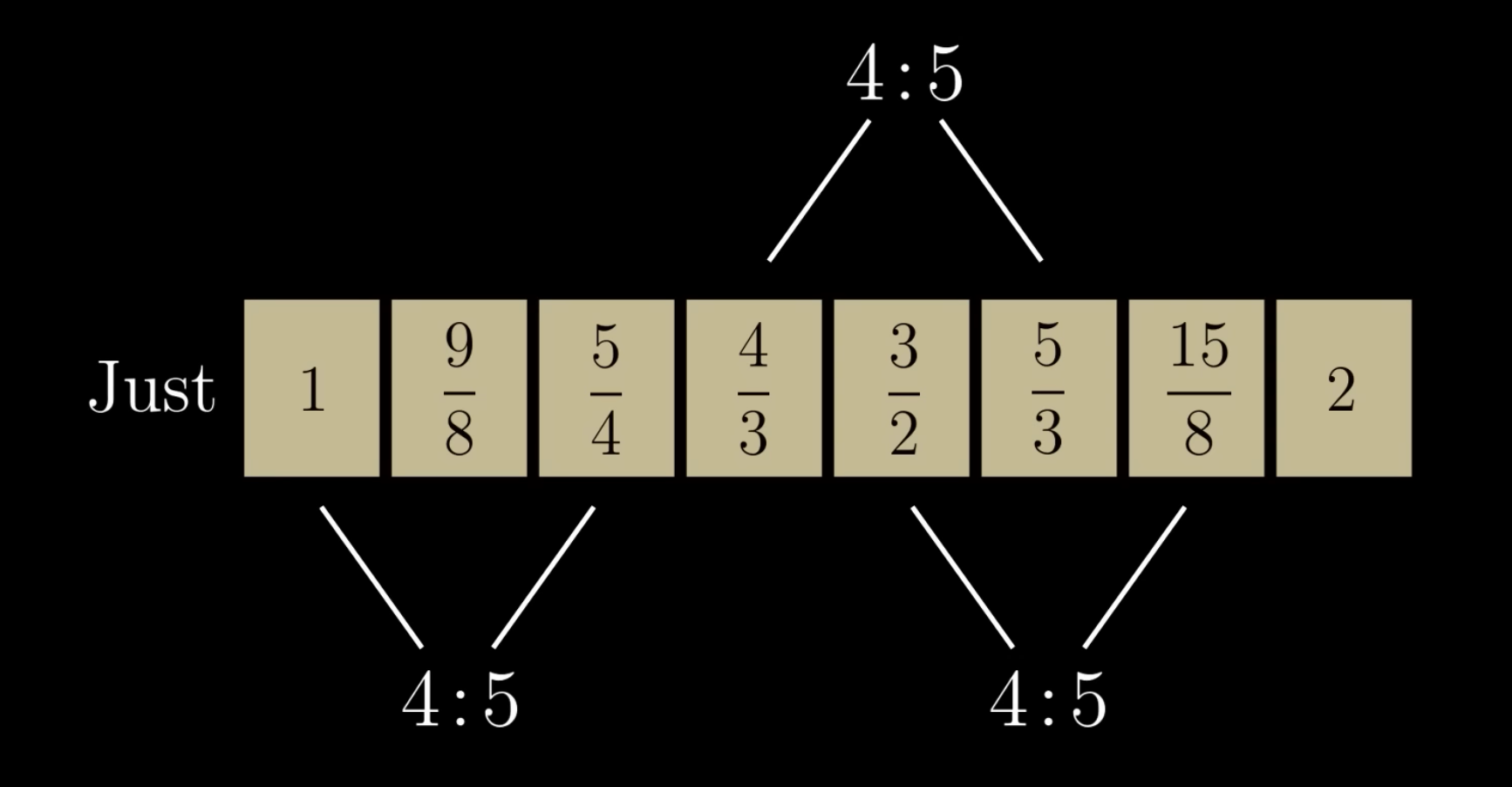
Just intonation §

Replaces the 3rd, the 6th, and the 7th using the correct ratio for the major third. Has much better harmonics.

However, since everything is tuned to the root, transposing becomes problematic.

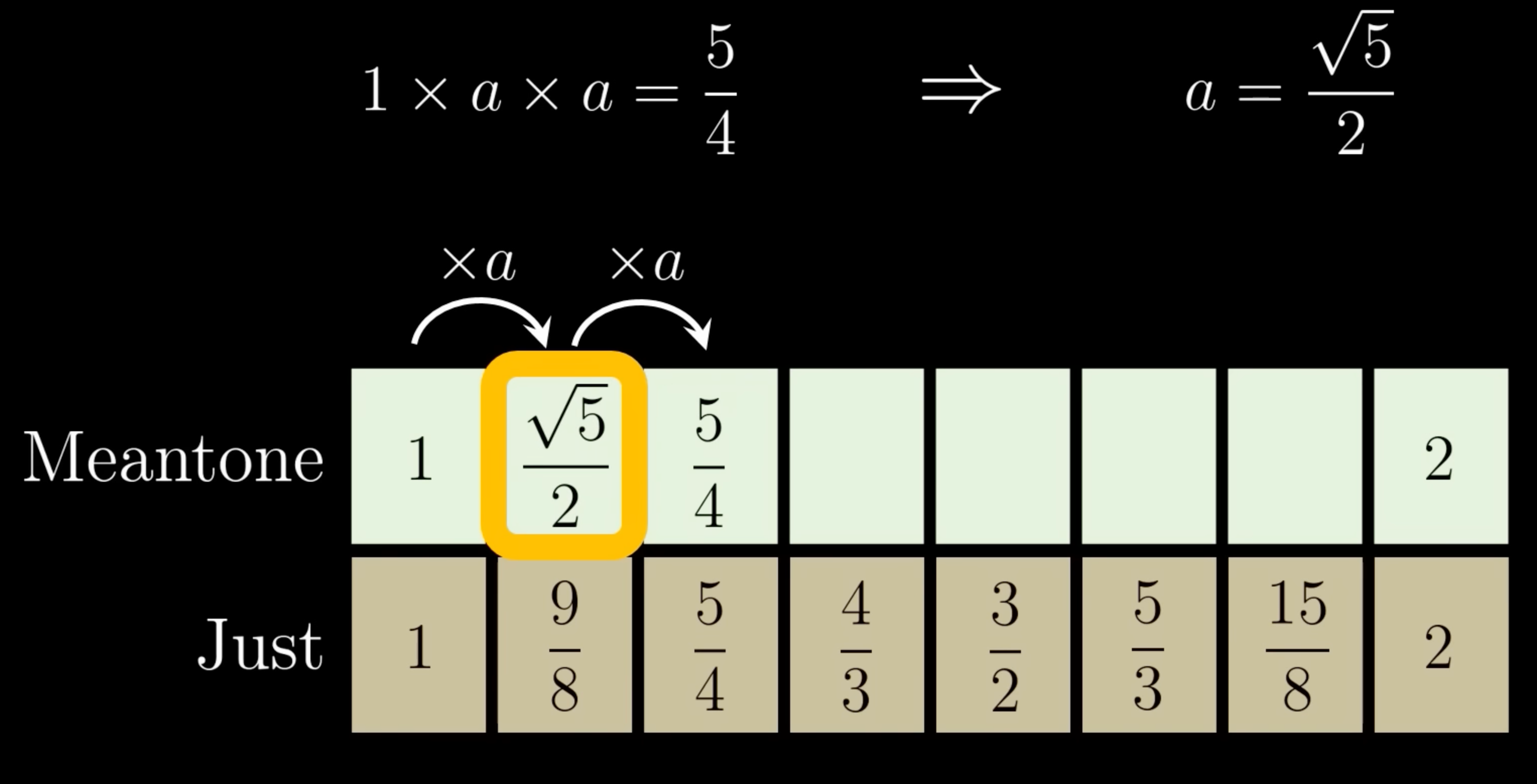
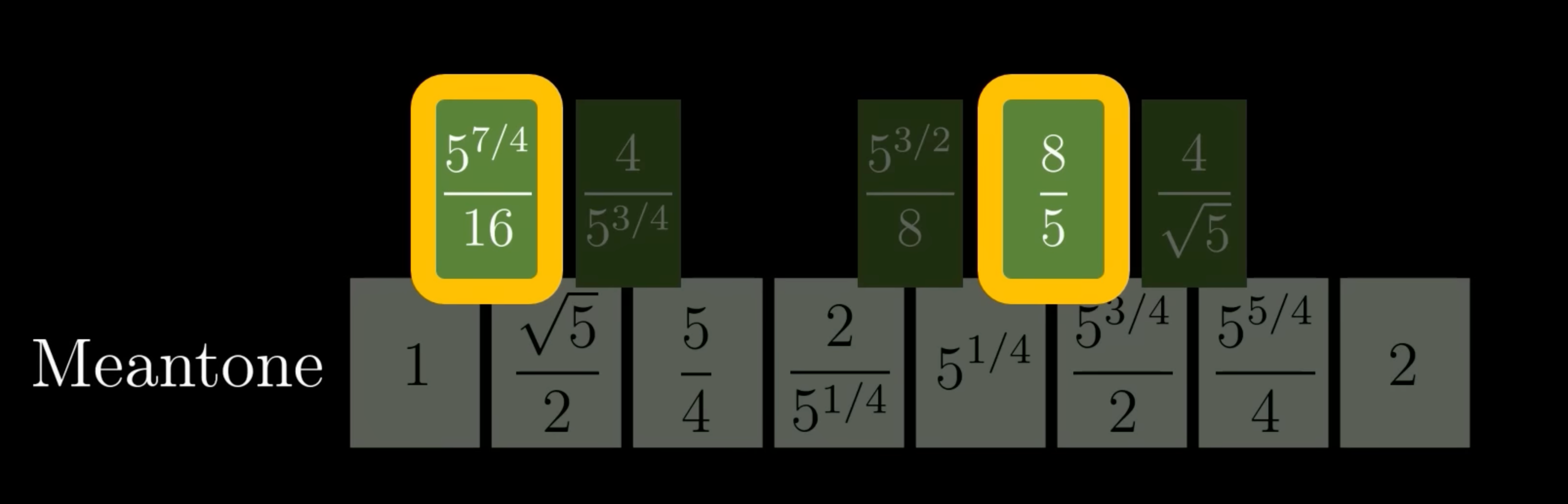
Meantone temperament §

Attempts to solve the transposition problem by using the geometric mean to ensure consistent interval ratios.

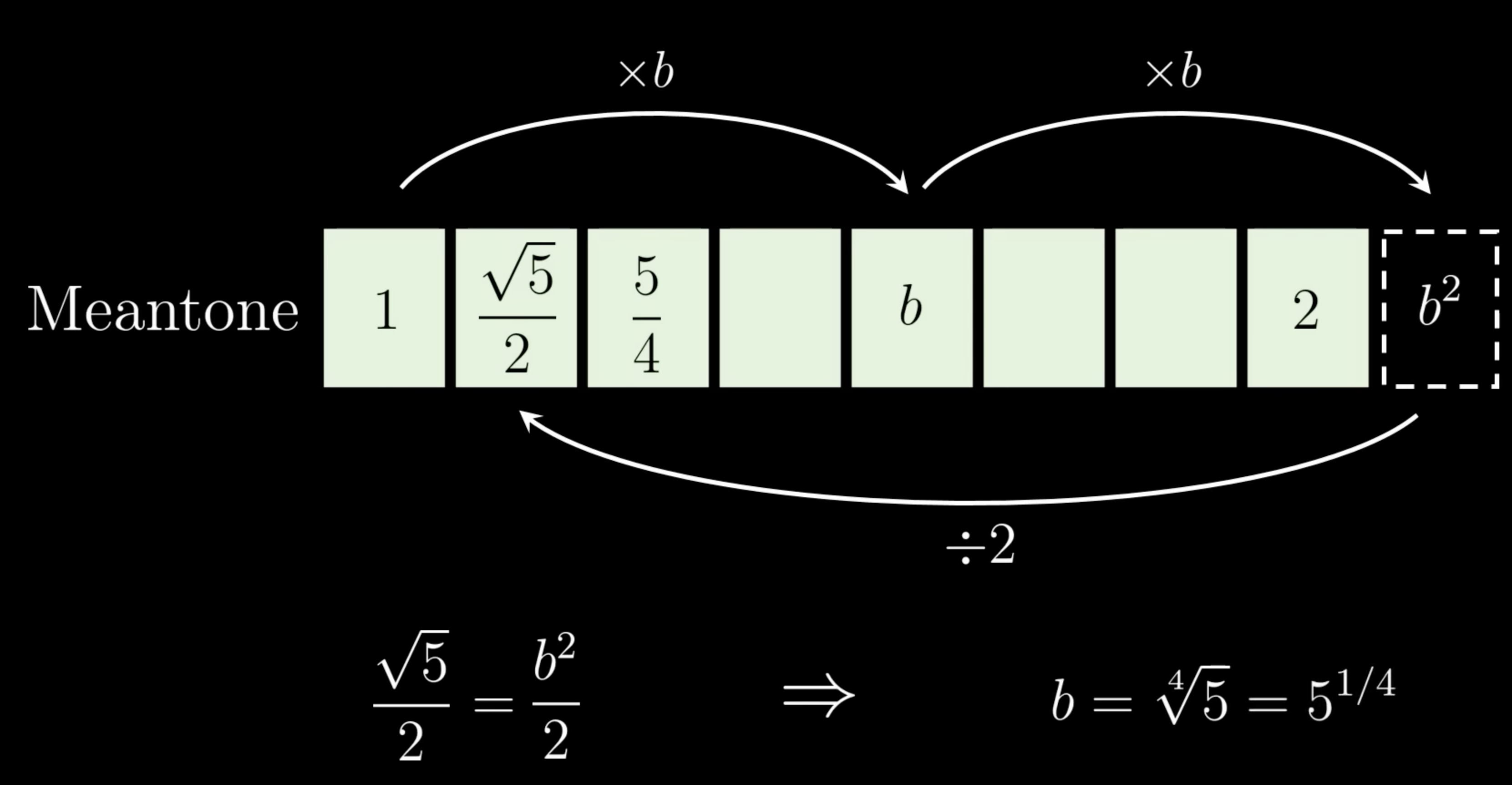
The problem with this is the wolf interval, which sounds terrible:

Equal temperament §

Adopted for convenience.

Pro: close approximations to the actual ratios.

$$\begin{array}{rl}& 2^{(0/12)}=1\leftarrow \text{unison}\\ & 2^{(1/12)}\approx 1.0595\\ & 2^{(2/12)}\approx 1.1225\\ & 2^{(3/12)}\approx 1.1892\\ & \\ & 2^{(4/12)}\approx 1.2599\approx 5:4\leftarrow \text{major 3rd}\\ & 2^{(5/12)}\approx 1.3348\approx 4:3\leftarrow \text{perfect 4th}\\ & 2^{(6/12)}\approx 1.4142\\ & 2^{(7/12)}\approx 1.4983\approx 3:2\leftarrow \text{perfect 5th}\\ & 2^{(8/12)}\approx 1.5874\\ & 2^{(9/12)}\approx 1.6818\\ & 2^{(10/12)}\approx 1.7818\\ & 2^{(11/12)}\approx 1.8877\\ & 2^{(12/12)}=2\leftarrow \text{octave}\end{array}$$

Con: not a single note is in tune. The major third is 14 cents too sharp (compared to JI tuning).

Below is the harmonic series. The numbers represent the cents needed to return to just intonation tuning

---

Implications:

• $E♯\ne F$
• Jacob Collier’s harmonies are out of this world because he uses JI and ignores computers.
• Perfect pitch: perfect memory of imperfectly tuned notes
• Jazz wouldn’t be possible without equal temperament, but when no key change is needed, no need to compromise on tuning.
• guitars with squiggly frets