dynamic programming

Taking a recursive algorithm and finding the overlapping subproblems (repeated calls), then caching those results for future recursive calls.

Some people only refer to bottom-up DP as DP, and call top-down DP as memoization

The following implementation of Fibonacci is not the most efficient:

int fibonacci(int i) {
    if (i == 0) return 0;
    if (i == 1) return 1;
    return fibonacci(i - 1) + fibonacci(i - 2);
} 

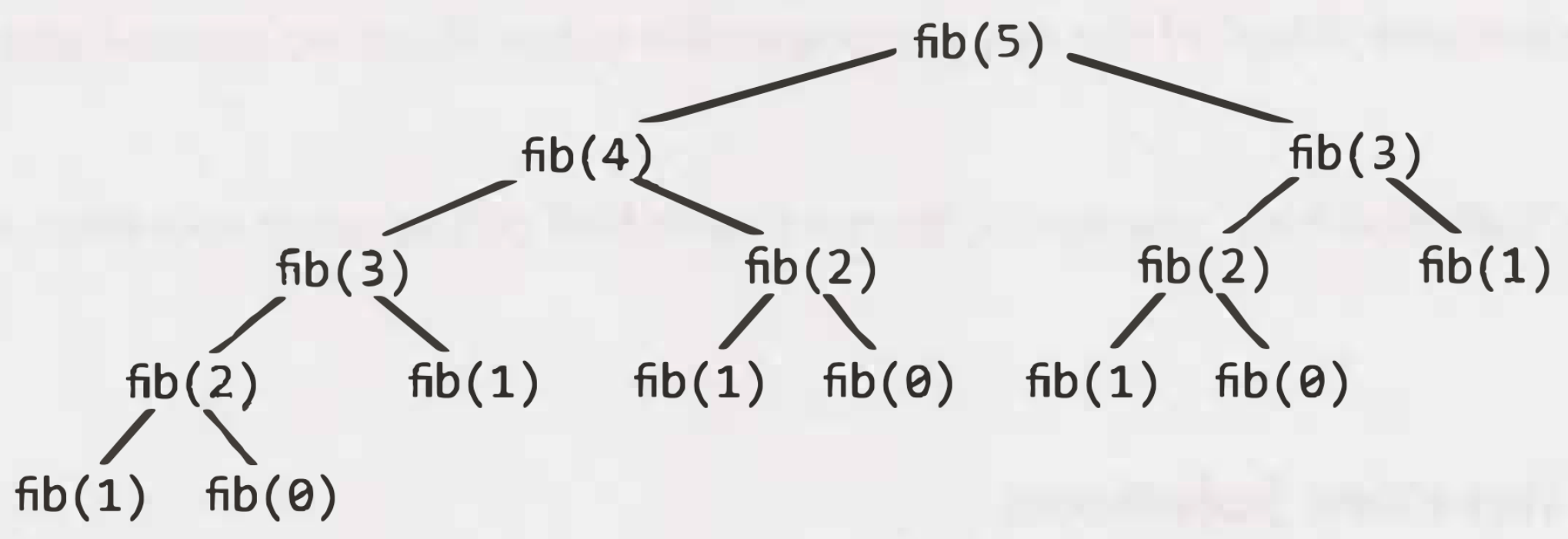
Roughly $2^n$ nodes, so the time complexity is $O(2^n)$

Top down approach (memoization) §

int fibonacci(int n) {
    return fibonacci(n, new int[n + 1]);
}
 
int fibonacci(int i, int[] memo) { # caching reduces repeated calls
    if (i == 0 || i == 1)
        return i;
    if (memo[i] == 0) {
        memo[i] = fibonacci(i - 1, memo) + fibonacci(i - 2, memo);
    }
    return memo[i];
}

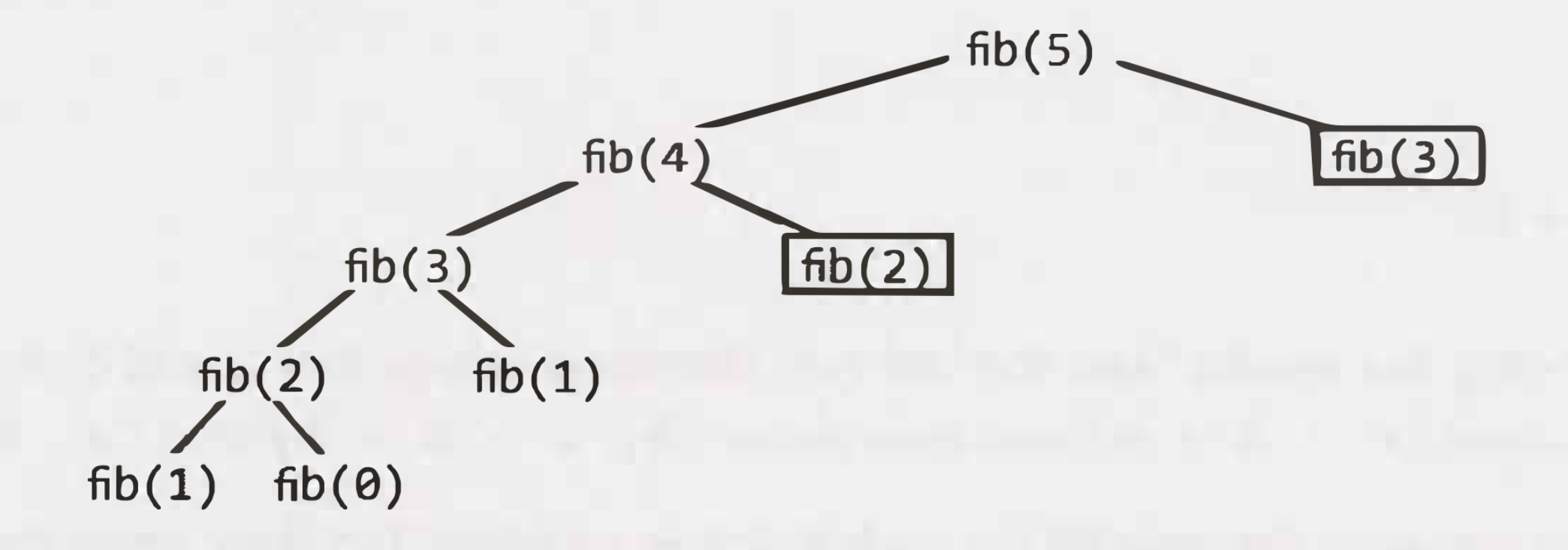
The black boxes represent cached calls that returned immediately. They require no work.

By using memoization, we can reduce the runtime to $O(n)$, since there are roughly 2n children.

Bottom up approach (tabulation) §

int fibonacci(int n) {
    if (n == 0)
        return 0;
    else if (n == 1)
        return 1;
    
    int[] memo = new int[n];
    memo[0] = 0;
    memo[1] = 1;
    
    for (int i = 2; i < n; i++) {
        memo[i] = memo[i - 1] + memo[i - 2];
    }
    
    return memo[n - 1] + memo[n - 2];
}
 

We can get rid of the memo table b/c we only use memo[i] for memo[i+1] and memo[i+2]

At each iteration, we compute the next value (c = a + b) and then move (b, c = a + b) into (a, b).

int fibonacci(int n) {
    if (n == 0)
        return 0;
 
    int a = 0;
    int b = 1;
 
    for (int i = 2; i < n; i++) {
        int c = a + b;
        a = b;
        b = c;
    }
 
    return a + b;
}

Example: climbing stairs §

memoization §

class Solution:
    @cache
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        
        return self.climbStairs(n-1)+ self.climbStairs(n-2)
        

class Solution:
    def __init__(self):
        self.memo = {}
    
    def climbStairs(self, n: int) -> int:
        if n in self.memo:
            return self.memo[n]
        if n <= 1:
            return 1
        
        self.memo[n] = self.climbStairs(n - 1) + self.climbStairs(n - 2)
        return self.memo[n]

class Solution:
    def climbStairs(self, n: int) -> int:
        
        memo = {1:1,2:2}
 
        def f(n):
            if n in memo:
                return memo[n]
            else:
                memo[n] = f(n-1) + f(n-2)
                return memo[n]
 
        return f(n)
        

dp §

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2:
            return n
        a=[1,2]
        for i in range(2,n):
            a.append(a[i-2] + a[i-1])
        return a[-1]

optimized dp §

class Solution:
    def climbStairs(self, n: int) -> int:
        if n <= 2: # optional
            return n 
 
        one, two = 1, 1
 
        for i in range(n-1):
            temp = one 
            one = one + two
            two = temp
 
        return one

Practice §

Classic problems §

• knapsack
• subset sum
• longest increasing subsequence
• longest common subsequence
• longest palindromic subsequence
• longest path in a DAG
• count all possible paths in a matrix
• edit distance
• rod cutting

Types §

• 1D
  • Fibonacci
  • max subarray (Kadane’s)
• 2D
  • unique paths and grid traversal
  • knapsack
    • 0/1:
      • target sum
      • partition equal subset sum
    • unbounded:
      • coin change
    • (fractional knapsack is greedy, not DP)
  • strings
    • LCS
    • palindromic substrings
    • string segmentation
    • LIS
• On trees